Home Pengetahuan Ayo Belajar Rumus Matematika Matriks dan Invers

May 28, 2013

Ayo Belajar Rumus Matematika Matriks dan Invers

Ayo Belajar Rumus Matematika Matriks dan Invers Memang pelajaran satu ini sangat di gemari oleh orang-orang alias pelajar bangsa Indonesia ini. Matematika banyak rumus-rumus gaib yang ada di dalamnya? Gaib-gaib apa? bukan gaib alias pemaham dalam rumus sedikit sulit tapi semua kesulitan itu dapat berhenti jika teman-teman mengerti bagaimana jalan rumus tersebut.

Nah untuk itu Seoanthrax berbagi sedikit pengetahuan tentang rumus yang satu ini yaitu Matriks dan Invers. Dalam Belajar Matematika "tentang Rumus Matriks dan Invers ini" teman-teman harus butuh konsentrasi terutama.dalam belajar Rumus Matriks ini jangan terlalu terburu pahami perkalian dan pemindahan angkanya. Berikut temanteman dapat belajar Matriks dan Invers di bawah :

Belajarlah dengan serius jangan sampai ada benda yang mengganggun konsentrasi di sekitar anda. Tetaplah berusaha memecahkan soal dengan sebaik mungkin. Selamat belajar.

JIka A dan B matriks bujur sangkar sedemikian rupa sehingga A B = B A = I , maka B disebut balikan atau invers dari A dan dapat dituliskan B = A − 1 ( B sama dengan invers A ). Matriks B juga mempunyai invers yaitu A maka dapat dituliskan A = B − 1. Jika tidak ditemukan matriks B, maka A dikatakan matriks tunggal (singular). Jika matriks B dan C adalah invers dari A maka B = C.

Matriks A = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} dapat di-invers apabila ad - bc ≠ 0
Dengan Rumus =
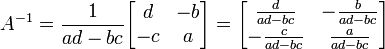
A^{-1} = \frac{1} {ad-bc}\begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix} = \begin{bmatrix} \frac{d} {ad-bc} & -\frac{b} {ad-bc} \\ -\frac{c} {ad-bc} & \frac{a} {ad-bc} \\ \end{bmatrix}
Apabila A dan B adalah matriks seordo dan memiliki balikan maka AB dapat di-invers dan (AB) − 1 = B − 1A − 1

Contoh 1:
Matriks

A = \begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix} dan B = \begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}
AB = \begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix}\begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = I (matriks identitas)
BA = \begin{bmatrix} 3 & 5 \\ 1 & 2 \\ \end{bmatrix}\begin{bmatrix} 2 & -5 \\ -1 & 3 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} = I (matriks identitas)
Maka dapat dituliskan bahwa B = A − 1 (B Merupakan invers dari A)

Contoh 2:
Matriks
A = \begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix} dan B = \begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}
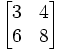
AB = \begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 3 & 4 \\ 6 & 8 \\ \end{bmatrix}
BA = \begin{bmatrix} 2 & 5 \\ 3 & 4 \\ \end{bmatrix}\begin{bmatrix} 1 & 1 \\ 3 & 4 \\ \end{bmatrix} = \begin{bmatrix} 17 & 21 \\ 15 & 19 \\ \end{bmatrix}
Karena AB ≠ BA ≠ I maka matriks A dan matriks B disebut matriks tunggal.

Contoh 3:
Matriks
A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \\ \end{bmatrix}
Tentukan Nilai dari A-1
Jawab:
A^{-1} =\frac{1} {(3)(2)-(5)(1)}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {6-5}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \frac{1} {1}\begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ -5 & 3 \\ \end{bmatrix}

Contoh 4:
Matriks
A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \\ \end{bmatrix}, B = \begin{bmatrix} 3 & 2 \\ 2 & 2 \\ \end{bmatrix}, AB = \begin{bmatrix} 7 & 6 \\ 9 & 8 \\ \end{bmatrix}
Dengan menggunakan rumus, maka didapatkan
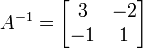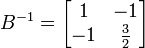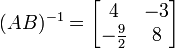
A^{-1} = \begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix}, B^{-1} = \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}, (AB)^{-1} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}
Maka
B^{-1} A^{-1}= \begin{bmatrix} 1 & -1 \\ -1 & \frac{3} {2} \\ \end{bmatrix}\begin{bmatrix} 3 & -2 \\ -1 & 1 \\ \end{bmatrix} = \begin{bmatrix} 4 & -3 \\ -\frac{9} {2} & 8 \\ \end{bmatrix}
Ini membuktikan bahwa (AB) − 1 = B − 1A − 1

Berikutlah Ilmu pengetahuan Matematika Rumus Matriks Invers yang dapat Seoanthrax sampaikan. Semoga dapat membantu teman-teman semua dalam mengerjakan tugasnya dari bu guru.intinya jika belajar itu pertama konsentrasi kalau bisa teman-teman harus fokus tenangkan diri jangan sampai lelah dan memaksa. Selamat Belajar. Go Prestasi !

Terimakasih telah membaca artikel yang berjudul Ayo Belajar Rumus Matematika Matriks dan Invers kali ini. Silahkan dapatkan artikel terbaru lainnya hanya di Seoanthrax. Jangan lupa untuk membagikan artikel ini di media sosial anda agar bermanfaat untuk orang banyak.

BAGIKAN TULISAN

REKOMENDASI TULISAN

Disqus Comments